SPSS 일원배치 분산분석 (one way ANOVA)
목차
1. 일원배치 분산분석
2. 분석방법
- 사후검정
3. 결과해석
일원배치 분산분석 (One-way ANOVA)
※ 한 종류의 독립변수가 적용된 서로 다른 3개 이상의 집단 간의 평균을 비교한다.
e.g.) 실험군 1(PNF)과 실험군 2(스트레칭), 대조군(중재 X) 3개 그룹의 각 중재 후 엉덩관절 굽힘 관절가동범위 변화에 대해 그룹별로 비교한다.
- 독립변수 : 운동 유형 (PNF & 스트레칭 & 중재 X)
- 종속변수 : 엉덩관절 굽힘 관절가동범위
기본조건
- 변수
- 독립변수: 질적변수 (명목척도, 순서척도)
- 종속변수: 양적변수 (비척도, 등간척도) - 세 집단이 서로 독립적이어야 한다.
- 세 집단이 모두 정규분포여야 한다.
- 세 집단의 분산이 모두 동일해야 한다.
가설검증
- 영가설 : 3개 그룹 간에는 서로 어떠한 차이도 없다 (p > 0.05).
- 대립가설 : 3개 그룹 간에는 최소 1개 이상의 차이가 있다 (p ≤ 0.05).
분석방법
1. 검정위치
분석 -> 평균 비교 -> 일원배치 분산분석
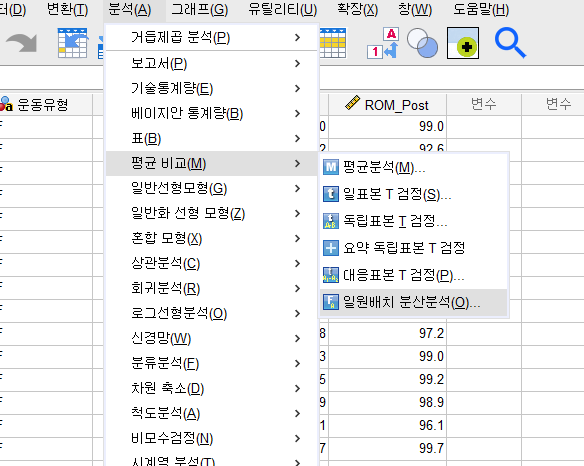
2. 검정 설정
'종속변수'에 변수 입력 -> '요인'에 독립변수 입력 -> 사후분석 클릭

3. 사후검정

용어 정리
- 검정력 : 검정력이 높을수록 실제로 발생한 차이를 더 잘 감지할 수 있다.
- 보수적인 검정방법 : 제1종 오류를 최소화하는 것이다.
- 제1종 오류 : 실제로는 차이가 없지만, 차이가 있다고 연구 결과가 나오는 오류이다.
- 검정 방법이 보수적일수록 통계적으로 유의미한 결괏값이 나올 확률이 줄어든다. - 검정력과 보수적인 검정방법은 대체로 반비례한다.
- 검정 방법이 보수적일수록 검정력이 낮다.
검정 방법
등분산이 가정된 경우
- Bonferroni : T 검정을 사용하며, t검정 반복시행으로 인한 1종 오류의 증가를 보정한 형태이다.
- n수 : 동일하지 않아도 된다.
- 특징 : 오류의 보정으로 인해 보수적으로 작용될 수 있다.
- 단점 : 그룹의 수가 많아질수록 검정력이 약해진다. - Tukey 방법 (Tukey's Honestly Significant Difference; HSD): F분포를 사용한다.
- n수 : 각 집단이 모두 동일해야 한다.
- 특징 : n수가 같은 경우 많이 선호된다.
- 단점 : 표본 수가 적을수록 검정력이 약해진다. - Scheffe : F분포를 사용한다.
- n수 : 동일하지 않아도 된다.
- 특징 : 표본이 클수록 검정력이 증가한다.
- 단점 : 큰 차이가 있어야 유의한 차이로 인정하는 매우 보수적인 방법이다. - Duncan : F분포를 사용한다.
- n수 : 각 집단이 모두 동일해야 한다.
- 특징 : 작은 차이를 구분해야 하는 경우에 선호된다.
- 단점 : 제1종 오류가 발생할 확률이 높다.
등분산이 가정되지 않은 경우
- Dunnett의 T3
- 표준화 최대 계수를 기준으로 하는 쌍대 비교 검정을 수행합니다.
- n수가 다른 경우 검정력이 더 높다.
- 제1형 오류의 통제가 강하다. - Games-Howell
- 경우에 따라 자유롭게 수행되는 쌍대 비교 검정입니다.
- n수가 다른 경우 사용가능
- 보편적으로 선호된다.
4. 선택사항
- '옵션'에서 기술통계 & 분산 동질성 검정 & 평균도표 체크
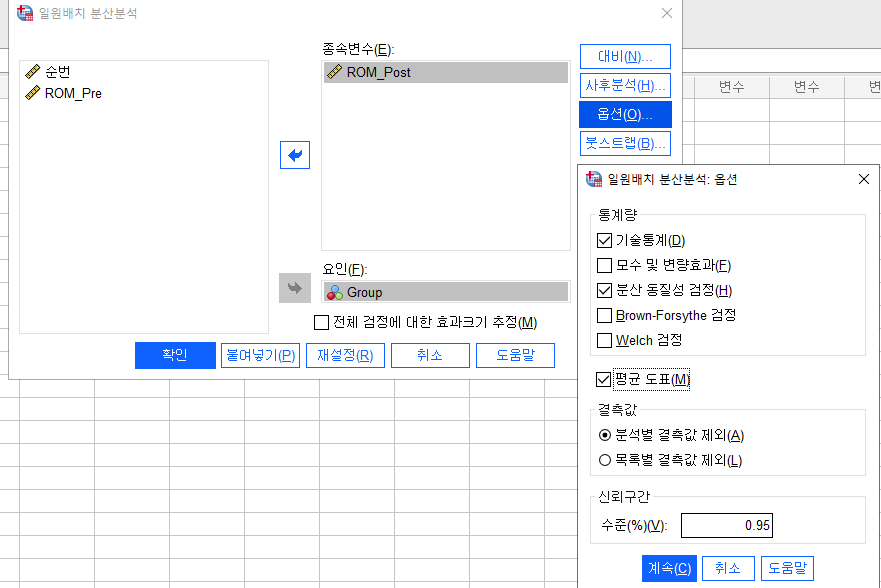
결과해석

Levene 등분산 검정
- 유의확률(p) ≥ 0.05 : 영가설(서로 차이가 없음) 채택으로 등분산을 가정한다.
- 유의확률(p) < 0.05 : 등분산을 가정하지 않는다.
- p값이 0.05 이상이기 때문에 '등분산을 가정함'에 대한 사후검정 결괏값을 확인한다.

- One way ANOVA에 대한 p값
'CTT 유의확률' = p값
- p ≤ 0.05 : 세 집단 간에 1개 이상의 유의미한 차이가 있다.
- p > 0.05 : 세 집단 간에 유의미한 차이가 없다.

- 각 사후검정에 따른 세 그룹의 그룹별 세부 p값
- 왼쪽 보라색 부분의 숫자는 세 그룹의 번호이다.
- e.g.1) Tukey HSD의 그룹 1(PNF)과 그룹 2(스트레칭) 간의 p값은 0.000으로 유의미한 차이가 있다(초록색 부분).
- e.g.1) Tukey HSD의 그룹 2(스트레칭)와 그룹 3(중재 X) 간의 p값은 0.002으로 유의미한 차이가 있다(하늘색 부분).
첨부파일
관련 참고자료
IBM SPSS 일원배치 분산분석:사후검정
https://www.ibm.com/docs/ko/spss-statistics/beta?topic=anova-one-way-post-hoc-tests
관련 글
2024.03.18 - [SPSS] - SPSS 분산분석 사후검정 종류 및 특징 / Post-hoc (one-way ANOVA)
